What is Impulse Response ?
Impulse response is a very important tool to analyse systems and can help us quickly know the output given by a system for any arbitrary input of our choice for special kinds of systems like the LTI systems. In this blog, we will understand the impulse response from the fundamentals and try to build on it to see some of it’s amazing uses.
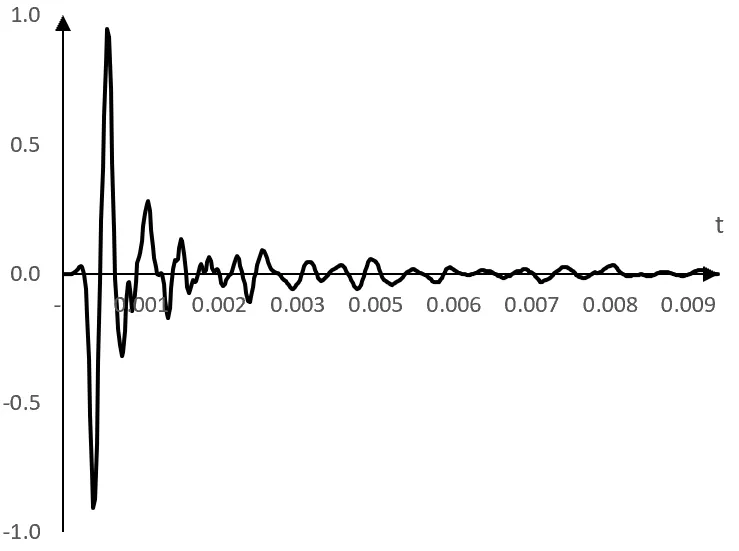 |
|---|
| Probable example for the Impulse Response of a System |
Literal Meaning
The word Impulse Response is fairly self-explanatory. Impulse response is the response given {output produced} by the system when the input is an impulse. That’s it!!
What is an Impulse now?
Impulse is a sudden high input given to a system such that it rises to a very large value and comes back to the initial {or any finite value} in a very small amount of time. Thus we can see that impulse is a momentary surge in the input provided to the system. Mathematical description of this impulse can be given using the Dirac Delta Distribution in continuous time {and Kronecker Delta Function in discrete time}.
Dirac Delta Distribution {Generalised function}
Dirac delta is not a function because it’s value is not defined at t = 1. It shows many interesting properties one of which is that it gives 1 when integrated over the entire real line. It displays many interesting properties, some of which are listed below —
 |
|---|
| Properties of the Dirac Delta Distribution |
Kronecker Delta {A detour in discrete time systems}
Kronecker delta is the discrete time counterpart of the continuous time Dirac Delta. As all of signal processing these days happens on a digital computer, it is important to understand kronecker delta as well. A point to note is that kronecker delta is a well-defined function and not a distribution like the dirac delta. It is defined as follows —
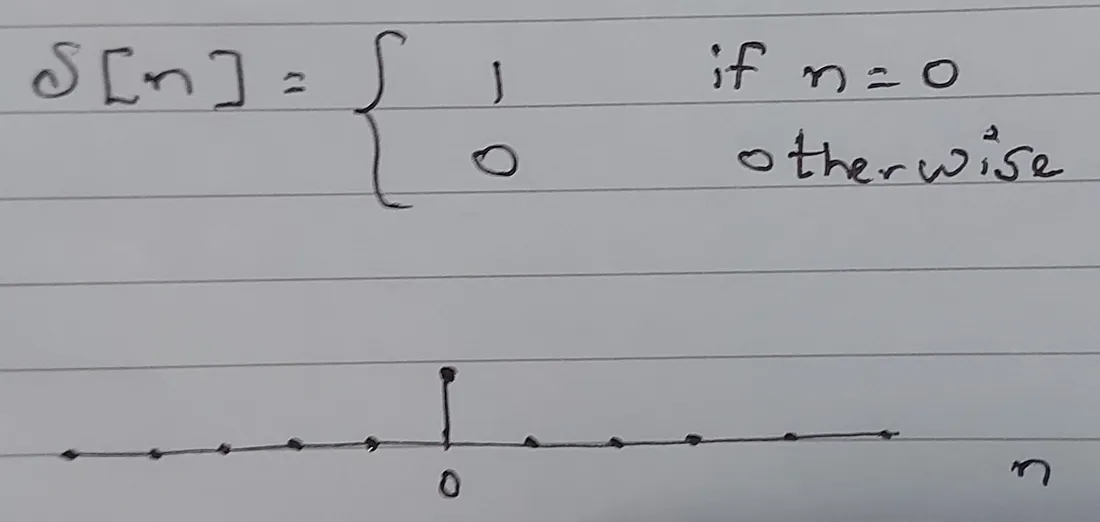 |
|---|
| Mathematical Definition of the Kronecker Delta Function |
Using Impulse response to find outputs of LTI systems
Now having understood what an impulse is and what impulse response actually means, we will see how we can make use of the knowledge of impulse response of an LTI system to figure out the output that the system will produce when given any arbitrary input.
 |
|---|
| Use of impulse response to compute the output of an LTI system |
Thus we can see, that by knowing just the impulse response of an LTI system we can compute the output that it will generate when given any arbitrary input of our choice. This is powerful, isn’t it??
Convolution
We came across this extremely important thing called Convolution in the previous section, which is used in all of Signal Processing and in Machine Learning {CNN is infact short form for Convolutional Neural Networks}. I would recommend you to watch this amazing video by the YouTube channel 3Blue1Brown to understand Convolution in great detail.
How to find the Impulse Response of a System
We understood how we can use the impulse response to compute the output of an LTI system to any arbitrary input. But a natural question might arise in your mind. How do we find out the Impulse response of a system in the first place? Figuring out the impulse response of a system directly can be tricky because no matter how well we try, we will never be able to produce an ideal dirac delta input. {Is this the end of the world?} We can be a little innovative and use the properties of an LTI systems to come up with a simple and elegant solution to compute the impulse response of the system using it’s step response.
What is a Unit Step input ?
This is a special kind of input which is fairly easy to generate {in electrical circuits it is just a constant DC voltage source} and has the power of giving us the impulse response of an LTI system through just a few mathematical manipulations. Unit step signal is denoted by u(t) in literature. Following is the mathematical definition of a unit step signal-
 |
|---|
| Mathematical definition of Unit step input |
Now, the unit step response of the system is just the output it produces when this is given as the input. We are now ready to use this step response to evaluate the impulse response.
Using Step Response to compute Impulse Response {only for LTI systems}
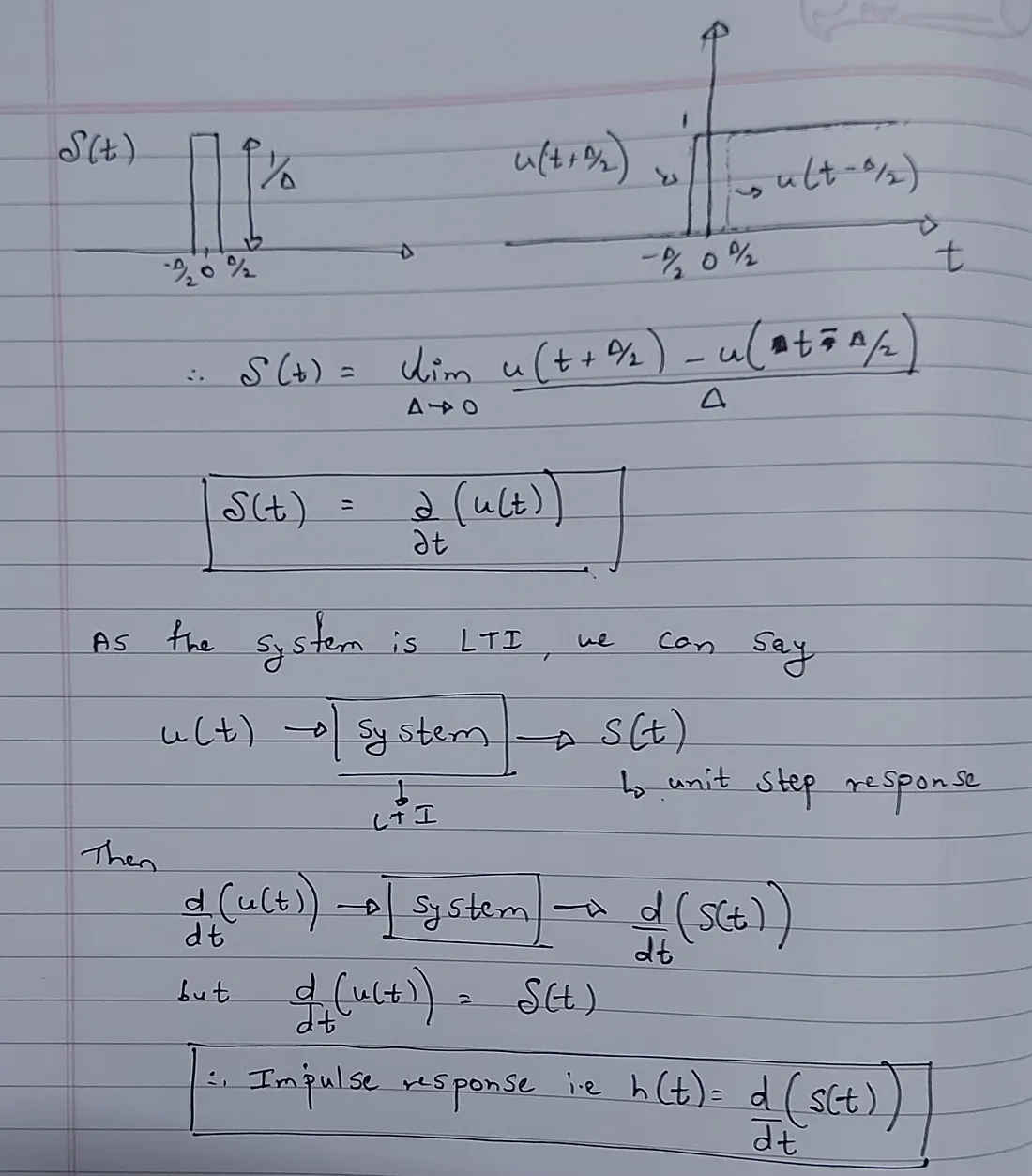 |
|---|
| Using step response to compute the impulse response |
We can see that impulse response is nothing but the derivative of the step response with respect to time {step response is usually much easier to find than the impulse response}. Now we will see 2 important applications where the impulse response of a system can be used to ascertain properties like Causality and BIBO stability of the system.
Impulse response for Causality
Causality in simple terms means that the output given by a system at a particular time should never be dependent on the value of the input at some later time. We can use impulse response of an LTI system to comment on it’s causality.
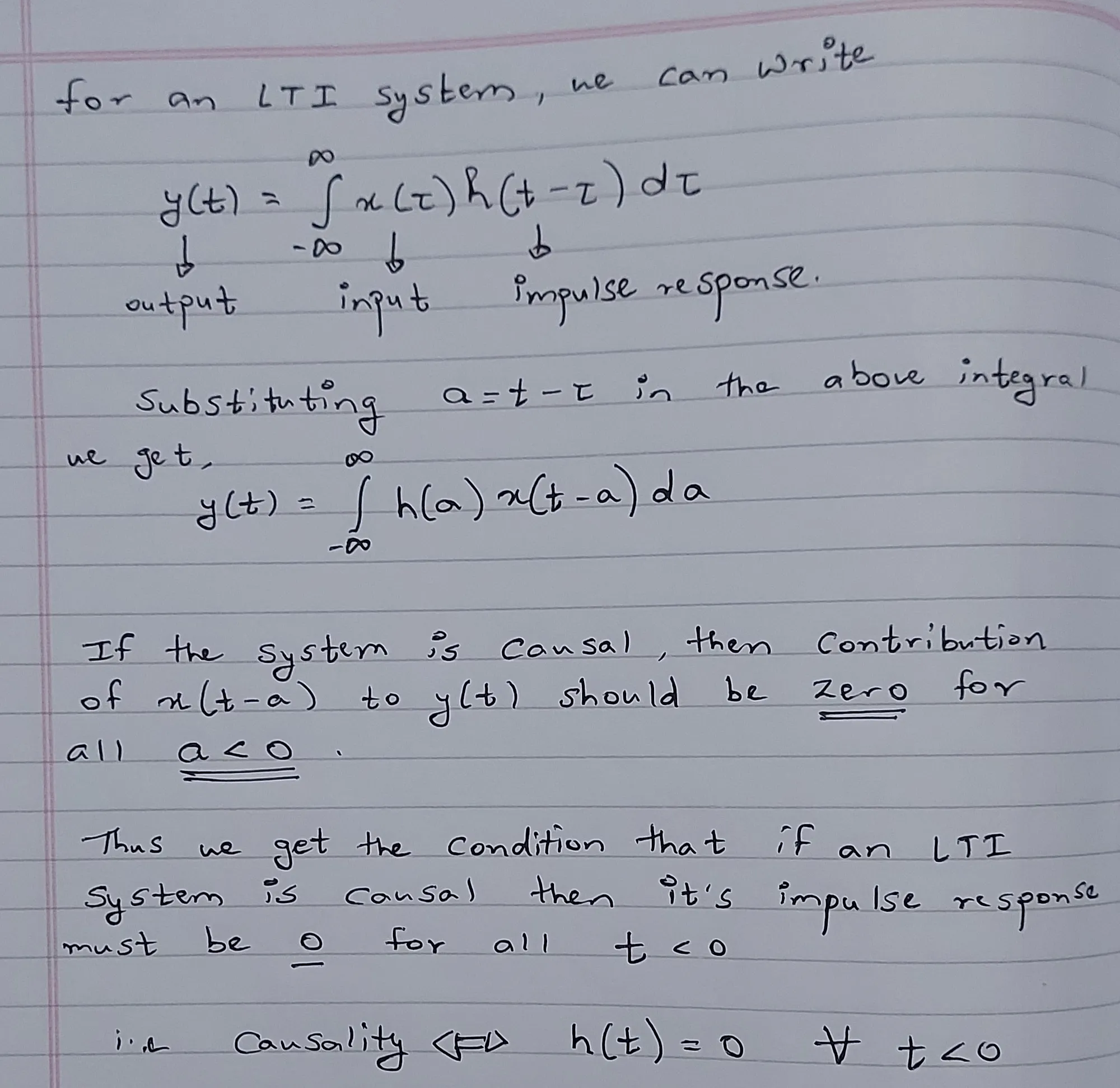 |
|---|
| Condition on Impulse response of an LTI system for Causality |
Impulse Response for BIBO stability of a system
BIBO stability means that the system output is bounded if it is provided with a bounded input. We can use the impulse response to comment on the BIBO stability of an LTI system.
 |
|---|
| Condition on impulse response of an LTI system for BIBO stability |
Absolute Integrability of the impulse response of the system is a necessary and sufficient condition for the system to be BIBO stable. Absolute integrability means that the integral should converge {it should be finite}.
Thus we can quickly check whether an LTI system is Causal and BIBO stable or not by just looking at it’s impulse response. This is how useful and powerful the impulse response is!!
Congratulations, you have come to the end of this blog!! I hope you enjoyed it and learnt a few important things about the Impulse Response of a system. {It is one of the most powerful tools to analyse the response of an LTI system to an arbitrary input}. Till now, we have analysed the continuous time systems in only the time-domain but we can perform all this analysis in frequency-domain too perhaps much more quickly. In the subsequent few blogs, we will discuss how to analyse continous time signals in the frequency-domain in great detail. Till then, Goodbye and keep enjoying Signal Processing!!